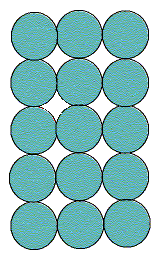
For a square lattice as shown, the coordination number is 4 (the number of circles touching any individual).  The coordination geometry is square, as shown below.
 

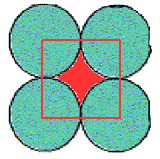
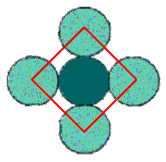
The empty spaces between the atoms are interstitial sites. Since each is touched by 4 circles, the interstitial sites are also 4-coordinate, and the geometry is also square.  In this example there are the same number of interstitial sites as circles.

Also because the atoms attract one another, there is a tendency to squeeze out as much empty space as possible. The packing efficiency is the fraction of the crystal (or unit cell) actually occupied by the atoms. It must always be less than 100% because it is impossible to pack spheres (atoms are usually spherical) without having some empty space between them.
 

Regarding our square lattice of circles, we can calculate the packing efficiency (PE) for this particular lattice as follows:

The interstitial sites must occupy 100% - 78.54% = 21.46%.

 
 
 
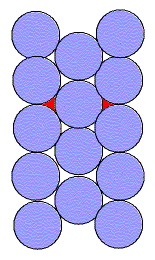
 Let us compare this with a hexagonal lattice of circles. We note that :

atomic coordination number = 6
atomic coordination geometry = hexagonal
interstitial coordination number = 3
interstitial coordination geometry = triangular
packing efficiency = 90.69%
interstitials = 9.31%

The larger coordination number (more bonds) and greater packing efficiency suggest that this would be a more stable lattice than the square one.
 
 

 

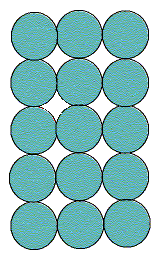
If we compare the square and hexagonal lattices, we see that both are made of columns of circles. However, in the hexagonal lattice every other column is shifted allowing the circles to nestle into the empty spaces. Thus, the higher packing efficiency.

Packing & Geometry

Except as otherwise noted, all images, movies and VRMLs are owned and copyright  by