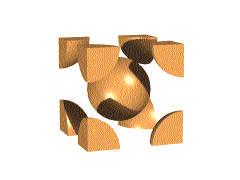
We can think of this unit cell as made by stuffing another atom into the center of the simple cubic lattice, slightly spreading the corners. Thus, the corner spheres no longer quite touch one another, but do touch the center. The diagonal through the body of the cube is 4x (sphere radius).
The packing efficiency of a bcc lattice is considerably higher than that of a simple cubic: 69.02 %
The higher coordination number and packing efficency mean that this lattice uses space more efficiently than simple cubic.
The unit cells stack together like this:
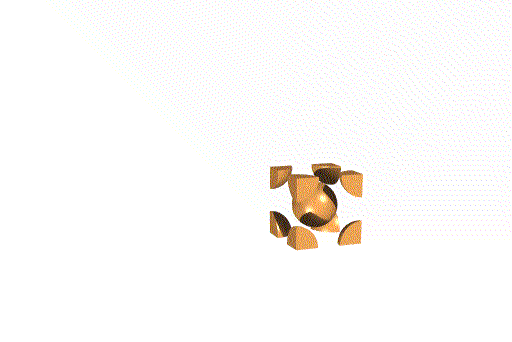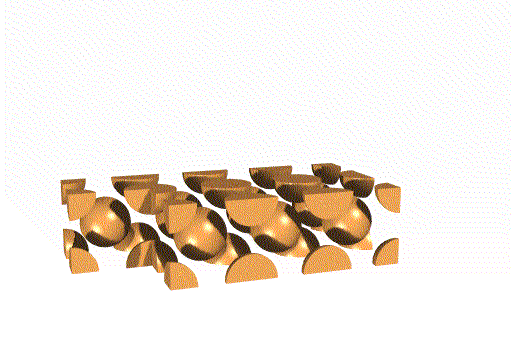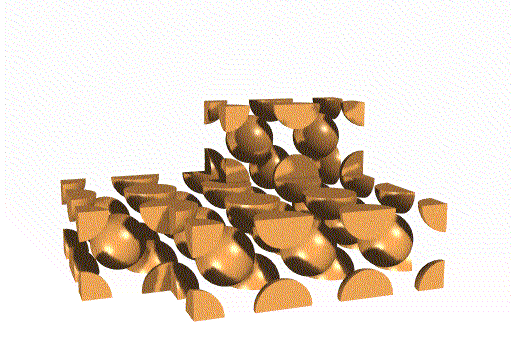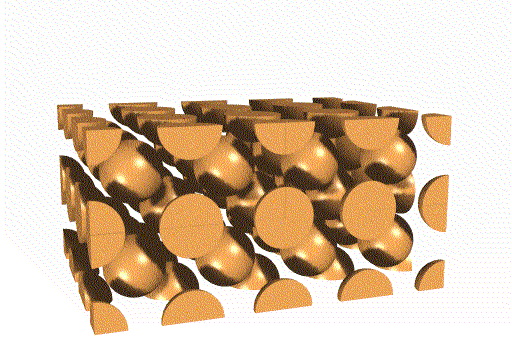
We can also think of this lattice as made from layers of square -
packed spheres. However, alternating layers stack so that the spheres "nestle
down" into the spaces between the spheres in the layer below. (Remember
that in a simple cubic lattice the spheres stack directly atop one another).
Body
Centered Cubic
by