The reason for the various colors is to help point out how the cells stack in the solid. Remember that the atoms are all the same.
The unit cell is again shown expanded for visibility. Actually, the corner atoms touch the one in the center of the face. The name "close packed" refers to the packing efficiency of 74.05%. No other packing can exceed this efficiency (although there are others with the same packing efficiency).
If we stack the cells into a lattice we notice that the atoms form diagonal layers - the reason for the colors is to make these stand out. Note that diagonal layers also form along our line of sight. Since these cut across the other layers, each layer will contain all three colors.
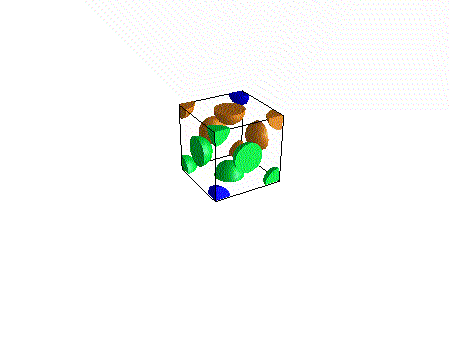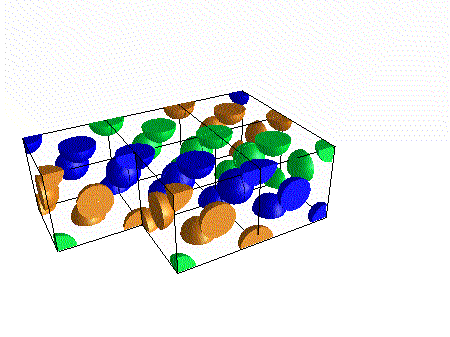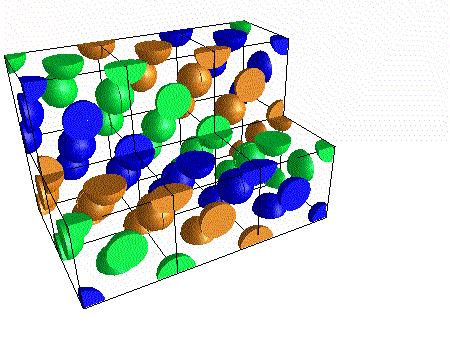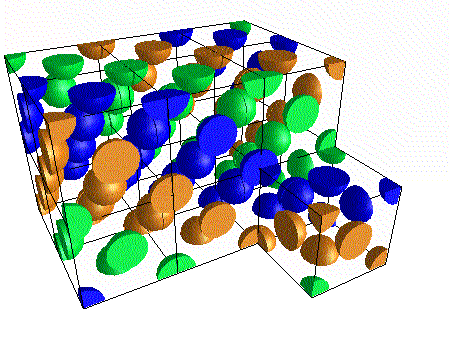
A different and better way of looking at this structure focuses on those layers.
We start with a hexagonal array of spheres (the blue "A" layer). Notice that this is a close-packed arrangement - there is no way to pack more spheres into a given area.

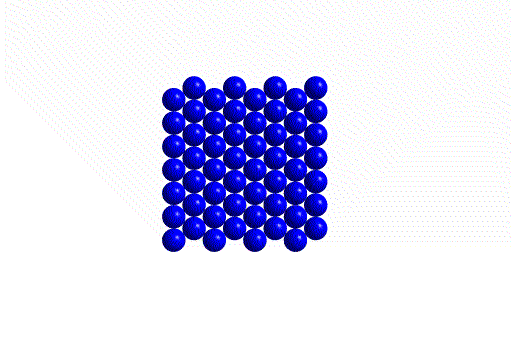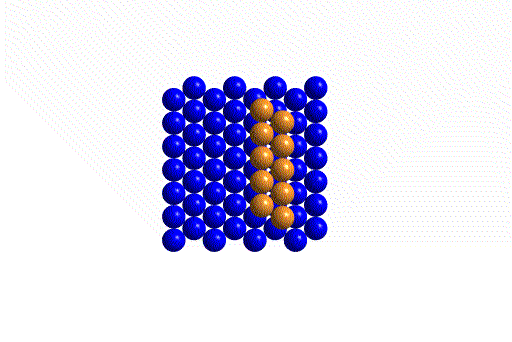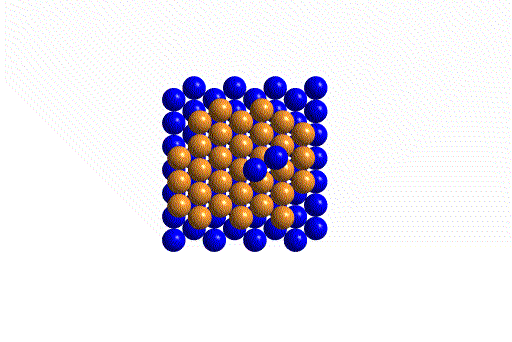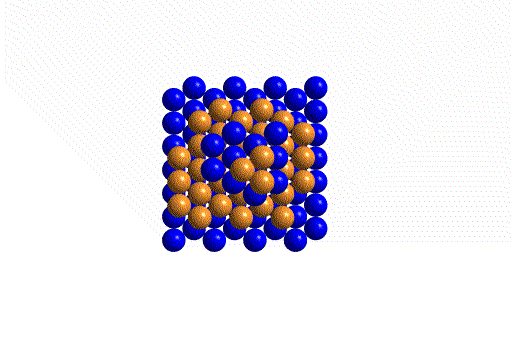
We then place a second close-packed layer (the gold "B" layer) atop the the first, so they nestle into the left-pointing holes in the first.
All spheres are actually the same atom, the colors are to help
you keep track of the layers.
Notice that there are 2 separate choices for the second layer; in the animation below, we have arbitrarily chosen to cover the left-pointing holes. We can put them over either all the "left-pointing" interstices or all the "right-pointing" interstices.
If we put them over the right-pointing interstices we generate a
different layer, labeled the green or "C" layer.
Remember there are twice as many interstitial
sites as spheres. (One left-pointing and one right-pointing).
We can continue to stack these layers in any order, providing that
no 2 identical layers are adjacent.



However, the internal structures and relationships can be examined
by moving the spheres apart slightly.


Remember, the gold atoms cover all the left-pointing interstices in the blue layer, and none of the right-pointing ones.
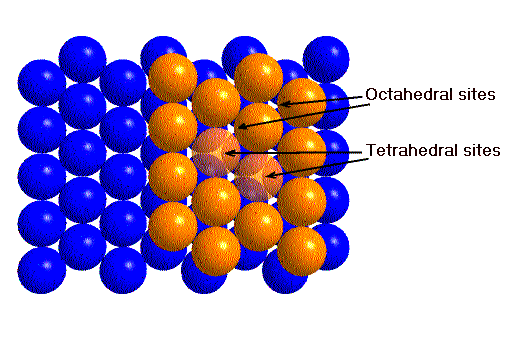
Under each gold atom is a small space surrounded by 4 atoms in a
tetrahedral arrangement. This is a 4 - coordinate tetrahedral interstitial
site.
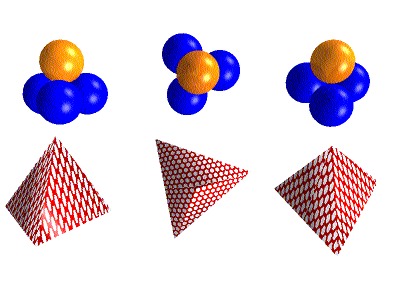
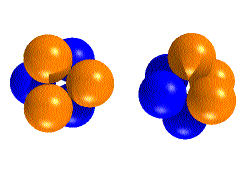
Go back and look at the lattice again and locate the tetrahedral
and octahedral interstitial sites.
Are there any cubic sites?
Examples of fcc / ccp metals include nickel, silver, gold, copper,
and aluminum.
Another way of stacking these layers is to omit the "C" layers altogether
- simply alternate "A" and "B". This is also a close-packed array, but
the symmetry is different. It is called:




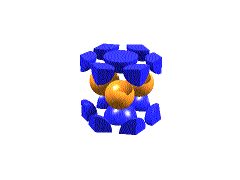

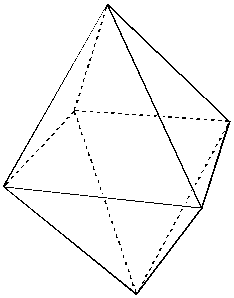
The coordination geometry about each atom is shown below. Note that while both structures have CN = 12 the arrangements are slightly different. In hcp, the top and bottom three are directly above one another. In ccp, they are staggered.
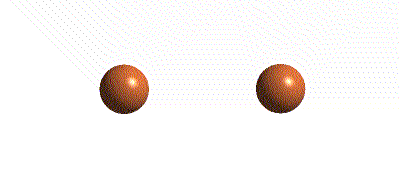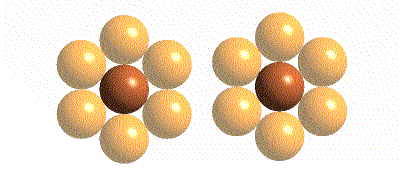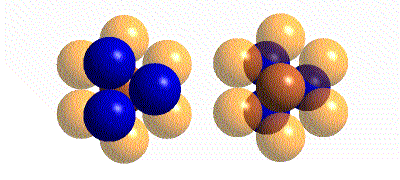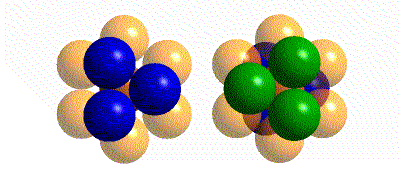


Below you see an actual STM image of a Ni surface. This is NOT a simulation, but a genuine picture. Note the hexagonal arrangement of atoms.
