CRYSTAL LATTICES
The most fundamental property of a crystal lattice is its symmetry. If we initially limit ourselves to 2 dimensions for simplicity, three types are:
Squares
![]()
Rectangles
![]()
Hexagons
![]()
![]()
![]() Squares
Squares

A square lattice may be visualized like this. 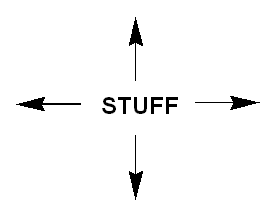
Each "stuff" represents a unit cell - the unit of repetition in the crystal.
If you were in one of the unit cells and looked out, you would see the same "stuff" at 0, 90, 180, and 270 degrees because a square repeats itself at 90 degree intervals - each 1/4 rotation.


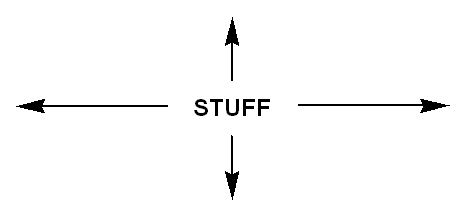
A rectangular lattice repeats at 0 and 180 degrees. We find "stuff" farther away at 90 and 270 degrees.




 A
square "eye" lattice.
A
square "eye" lattice.
 A square "foot" lattice.
A square "foot" lattice.

Look again at the "stuffed" hexagons. Notice that the unit cells completely fill the surface.
If the unit cells were seen in 3 dimensions, they would completely fill the space.
This is an important restriction as it prevents certain arrangements
such as pentagonal unit cells, as shown below.
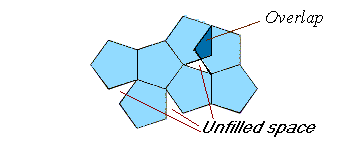
Do you see that this type of arrangement is not possible?
The unit cells must completely fill the surface and have no overlap.
In 3 dimensions, the ideas are similar; unit cells stack like boxes, filling the space, making the crystal.
The different colors are just to show the separate boxes - each unit
cell is identical.
Cubic Hexagonal

![]()
![]()
![]()

Click here to go to the next page.
Structure of Crystals
![]() Crystal
Lattices
Crystal
Lattices![]()
Unit Cells
From Unit Cell to Lattice
From Lattice to Unit Cell
Stoichiometry
Packing & Geometry
Simple Cubic Metals
Close Packed Structures
Body Centered Cubic
Cesium Chloride
Sodium Chloride
Rhenium Oxide
Niobium Oxide
![]()
Except as otherwise noted, all images, movies and
VRMLs are owned and copyright ![]() by
by
Barbara L. Sauls and Frederick C. Sauls 2000.
Contact the owners for individual permission to
use. blsauls@kings.edu