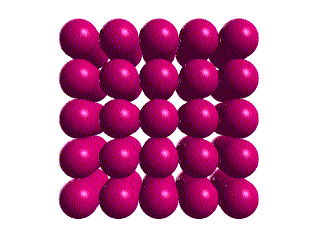SIMPLE CUBIC METAL
In a metal the atoms are all identical, and most are spherical (the
bonding does not depend on direction). Metals thus tend to adopt relatively
simple structures. The simplest is:
Simple Cubic (sc)

 Here are two ways to draw a unit cell for the simple cubic structure.
In the unit cell on the left, the atoms at the corners are cut because
only a portion (in this case 1/8) belongs to that cell. The rest of the
atom belongs to neighboring cells, as shown in the stacking below.
Here are two ways to draw a unit cell for the simple cubic structure.
In the unit cell on the left, the atoms at the corners are cut because
only a portion (in this case 1/8) belongs to that cell. The rest of the
atom belongs to neighboring cells, as shown in the stacking below.
Click on the left unit cell above to view a movie of it rotating.
Here we see the two unit cells stacked to form the lattice. 
 Notice that in each case the same overall structure is found.
Notice that in each case the same overall structure is found.


The movie below will give you a feel for the overall lattice
pattern.
Click on the image to view it.
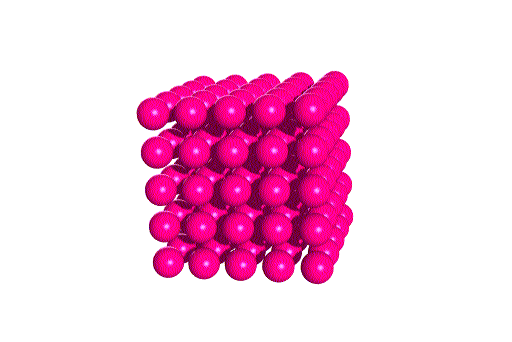 We can think of this lattice as layers of square packed spheres. The
layers are stacked so that each sphere is directly above the one in the
layer beneath.
We can think of this lattice as layers of square packed spheres. The
layers are stacked so that each sphere is directly above the one in the
layer beneath.
Although we have shown space between the spheres, this is only to
"open up" the structure to view. In the real crystal, the spheres touch
as shown in the unit cell and lattice below.
Thus, the edge length of the cell is 2x the sphere radius.

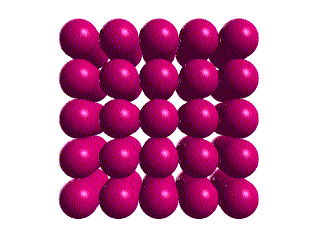
 Click on the unit cell and lattice above to view them rotating.
Click on the unit cell and lattice above to view them rotating.
In 3-D the packing efficiency is given by:

P.E. = (volume of spheres) / (volume of cell)
 For a simple cubic lattice, this is:
P.E. = (1/8x8)(4/3 pi r3) / (2r)3 =
pi/6 = 52.35%.
For a simple cubic lattice, this is:
P.E. = (1/8x8)(4/3 pi r3) / (2r)3 =
pi/6 = 52.35%.
This low value is not suprising. Remember that a 2-D square lattice
uses space inefficiently. A simple cubic lattice is its 3-D analog, and
also contains much empty space.
Let us shift our attention to the empty spaces in the lattice. Each
unit cell contains one large interstitial site in its center (47.65% of
the volume). There are 8 atoms touching this space, so the
interstitial coordination number is 8, and its geometry
is cubic (a cube has 8 corners).
 Since each unit cell contains (8 x 1/8 =) 1 atom and 1 interstitial
site, the number of atoms and interstitial sites is the same.
Since each unit cell contains (8 x 1/8 =) 1 atom and 1 interstitial
site, the number of atoms and interstitial sites is the same.
Examine the structure below which shows the arrangement about any
single atom in the simple cubic lattice; note that each atom has
6 neighbors, so the atomic coordination
number is 6. The coordination geometry is
octahedral (an octahedron has 6 corners).


Octahedral coordination of an atom.  An
octahedron.
An
octahedron.










Since both the coordination number and packing efficiency are low,
a simple cubic lattice uses space inefficiently. Very few examples of simple
cubic lattices are known (alpha - polonium is one of the few known simple
cubic lattices).
Below we again see a section of the simple cubic lattice as it
"really" is - with the atoms touching one another. Note the channels
formed by the alignment of the interstitials. These empty spaces can allow
other small atoms to enter the crystal.
Click on the image below to view the lattice.
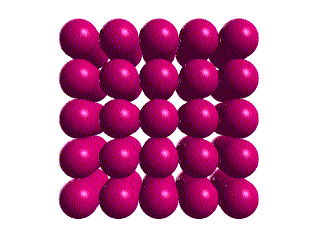

Click here to go to
the next page.
 Structure of Crystals
Crystal Lattices
Unit Cells
From Unit Cell to Lattice
From Lattice to Unit Cell
Stoichiometry
Packing & Geometry
Structure of Crystals
Crystal Lattices
Unit Cells
From Unit Cell to Lattice
From Lattice to Unit Cell
Stoichiometry
Packing & Geometry
 Simple
Cubic Metals
Simple
Cubic Metals Close Packed Structures
Body Centered Cubic
Cesium Chloride
Sodium Chloride
Rhenium Oxide
Niobium Oxide
Close Packed Structures
Body Centered Cubic
Cesium Chloride
Sodium Chloride
Rhenium Oxide
Niobium Oxide
 Except as otherwise noted, all images, movies
and VRMLs are owned and copyright
Except as otherwise noted, all images, movies
and VRMLs are owned and copyright  by
Dr. Barbara L. Sauls and Dr. Frederick C. Sauls
1998.
Contact the owners for individual permission
to use. barbarasauls@kings.edu
by
Dr. Barbara L. Sauls and Dr. Frederick C. Sauls
1998.
Contact the owners for individual permission
to use. barbarasauls@kings.edu






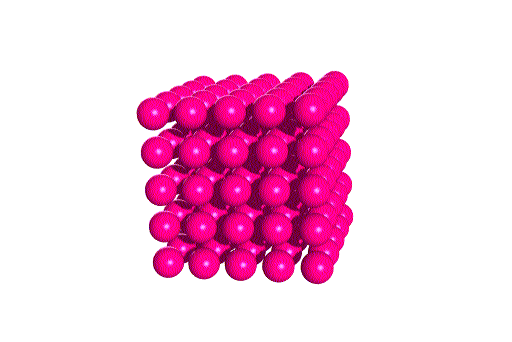

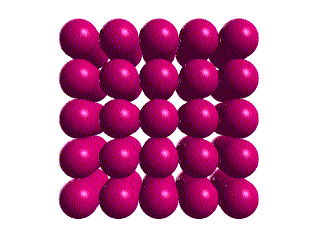
![]()

![]()

![]() An
octahedron.
An
octahedron.
![]()

![]()
![]()

![]()
![]()
![]()
![]()
![]()